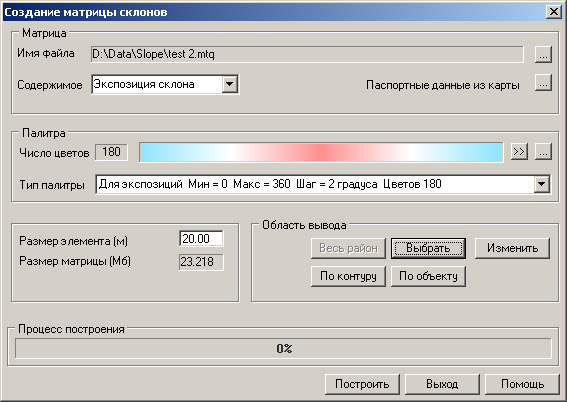
Building a matrix of slopes

In solving land management and design-survey tasks, there is a need to determine the directions of slope surfaces in the terrain. For this purpose, a quality matrix (*.MTQ) is constructed, reflecting the orientation of the terrain slopes. The task can be accomplished with the presence of a relief model — height matrix MTW, irregular point cloud MTD model, TIN model. The task generates the quality matrix MTQ, where elements can have values of slope angle or slope aspect, depending on the selected mode of operation.

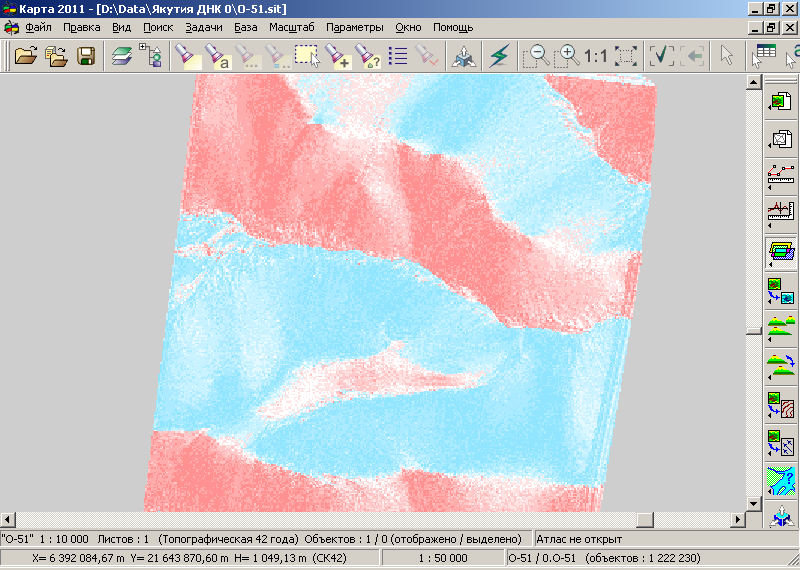
Depending on the "Content" mode, the elements of the created matrix will have values of slope angles or slope aspects.

The matrix records slope angle values in degrees: negative values are recorded for northern slopes (shades of blue palette), positive values for southern slopes (shades of pink palette), and values close to zero for flat areas (white color of the palette).

Construction of slope matrix:

The slope angle value for the determined element with center coordinates (x0, y0) is calculated using three heights:  

— the height at the determined point (x0, y0);  

— the height at the northern point relative to the determined one (xN, yN);  

— the height at the southern point relative to the determined one (xS, yS).  

The coordinates of the northern (xN, yN) and southern (xS, yS) points are calculated using the "north-south" direction taking into account the ecliptic tilt (22.5 degrees).  

Coordinates of the northern point:  

xN = x0 + Elem;  

yN = y0 + Dy.  

Coordinates of the southern point:  

xS = x0 - Elem;  

yS = y0 - Dy;  

where:  

Dy = Elem * tan(22.5);  

Elem - the side length of the matrix element in meters;  

tan(22.5) - tangent of the angle 22.5 degrees.  

The request for averaged absolute height values from the MTW height matrix is performed using the triangle method with the heights of elements surrounding the given point.  

The slope exposure value is one of the 16 direction angles, having the largest absolute slope angle. The slope exposure is measured in degrees and has a value equal to i * 22.5 where i ranges from 0 to 15. Exposure is the angle between the "north direction" and the "slope direction." The slope direction is one of the 16 directions around the given point (x0, y0), corresponding to the maximum absolute slope angle of the surface. The north direction is the X-axis vector of the map rotated clockwise by an angle ECLIPTIC = M_PI/8 (22.5 degrees).