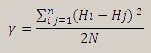Кригинг

Кригинг – это более гибкий по сравнению с логарифмической интерполяцией метод моделирования. Также как и логарифмическая интерполяция, кригинг строит сглаженную поверхность, но в кригинге пользователь может выбирать и настраивать моделирующую функцию. Поверхность, построенная с использованием кригинга, может, как касаться опорных точек, так и отличаться по высоте от опорных точек для сглаживания ошибочных измерений (см. далее Самородок).

В кригинге для анализа существующего распределения данных используются графики вариограммы - функции, вычисляемой по разности значений  высот пар точек, сгруппированных в лаги (группы) по взаимному расстоянию между точками.Вариограмма является мерой корреляции между соседними точками, т.е. характеризует насколько соседние точки похожи друг на друга по значению моделируемой характеристики.

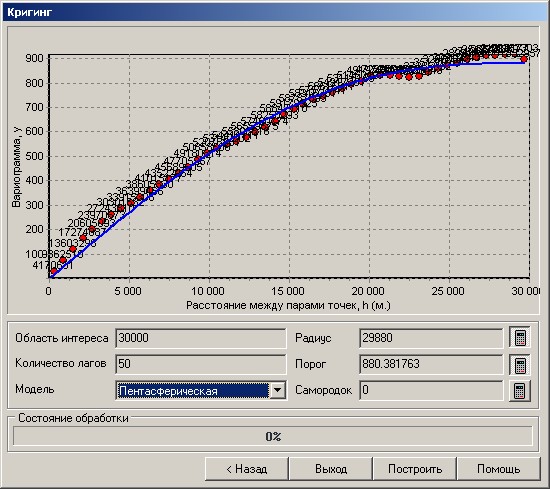
g - вариограмма для лага, содержащегоnточек (например, первый лаг включает пары точек, расстояния между которыми от 0 до 100 метров, второй лаг включает пары точек, расстояния между которыми от 100 до 200 метров, и т.д.);

Hi,Hj – значение моделируемой характеристики для пары точекi, j;

N – количествопар точек в лаге.

Вариограмма вычисляется для каждого лага и показывается на графике точками. Над каждой точкой графика показывается количество пар точек, по которым вычислялось значение вариограммы. Горизонтальная ось графика соответствует расстоянию между точками, а вертикальная значению вариограммы.

На основе этих данных исследователю нужно подобрать функцию, график которой максимально приближен к исходному графику (подобрать теоретическую вариограмму, моделирующую эмпирическую вариограмму).

Пример использования

При инициализации диалога кригингавыполняются следующие этапы:

- считываются координаты точек объектов, имеющих моделируемую характеристику;

- определяется максимальное расстояние между точками, которое используется для вычисления размера лага (количество лагов по умолчанию равно 50);

- для каждого лага вычисляется значение эмпирической вариограммы, которое отображается на графике точкой с подписью количества пар точек, попавших в лаг;

- вычисляются параметры принятой по умолчанию сферической модели. Вычисленная теоретическая вариограмма отображается на графике синей линей.

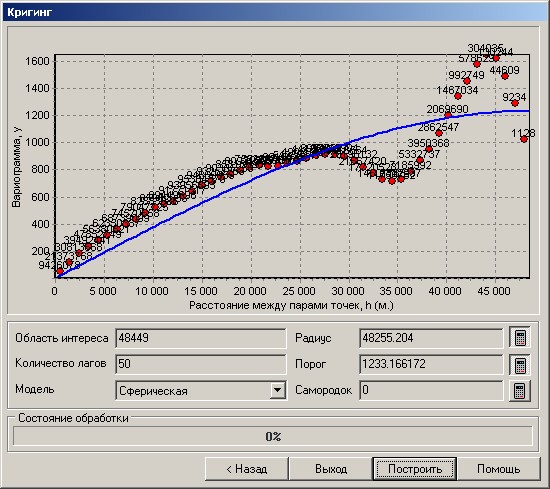
На представленном графике видно, что значение вариограммы возрастает, пока расстояние между точками не станет равным примерно 30000, а затем начинает колебаться. Это говорит о том, что точки, находящиеся на расстоянии больше 30000, не коррелируют друг с другом.

Уменьшим область интереса (исследуемый диапазон расстояний), введя 30000 в поле Область интереса.

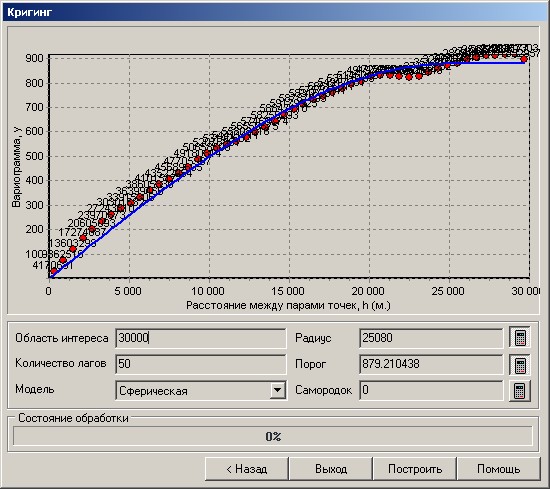
Теперь выберем модель из списка допустимых моделей, подходящую по форме графика эмпирической вариограммы. В данном случае больше всего подходит экспоненциальная модель.

Для анализа отдельных областей на графике можно выполнить его масштабирование, выделив нужную область «резиновым прямоугольником» сверху-вниз. Сдвиг увеличенной области относительно всего графика выполняется перемещением мыши при нажатой правой кнопке. Для возврата в исходный масштаб нужно снова выбрать резиновый прямоугольник, но в это раз в направлении  снизу-вверх.

Управлять формой графика теоретической вариограммы можно, изменяя параметры модели – радиус, порог, самородок (по умолчанию эти параметры вычисляются автоматически по точкам эмпирической вариограммы).

Радиус влияния модели– расстояниемежду парами точек, при котором график теоретической вариограммы становится горизонтальным.

Порог - значение, которое модель вариограммы принимает в точке радиуса влияния (значение по оси y) минус самородок.Порог и радиус моделирующей функции влияют на кривизну создаваемой поверхности.

Самородок – значение вариограммы для пар точек, расстояние между которыми равно нулю. Теоретически для одних и тех же точек значение вариограммы должно быть равно нулю (см. формулу). Однако на бесконечно малых расстояниях разница между измерениями зачастую не стремится к нулю. Этот факт носит название эффекта самородка.

Эффект самородка может быть отнесен за счет ошибок измерений или наличия природных факторов, допускающих возникновение неожиданного появления выбросов на расстояниях меньших, чем интервал выборки (или за счет обоих явлений). Обычно значение самородка принимается равным нулю. В этом случае высота построенной поверхности на опорных точках будет равна высоте этих точек.

В случаях, когда кривая явно стремится пересечь вертикальную ось графика выше нуля, можно установить ненулевое значение самородка.В этом случае поверхность будет не дотягиваться по высоте до опорных точек (поверхность будет сглажена в окрестности опорных точек). Причемсглаживание опорной точки тем больше, чем больше эта точка отличается от соседей. Поэтому использование ненулевого самородка фактически позволяется выполнить построение поверхности с исключением ошибок измерений моделируемой характеристики на опорных точках.  

Любой из трех параметров можно вычислять автоматически, либо ввести вручную. После изменения параметра происходит перерисовка графика. Изменяя вручную параметры, можно добиться лучшего приближения графика модели в нужной области.

После подбора параметров модели запуск построения матрицы выполняется нажатием кнопки Построить.