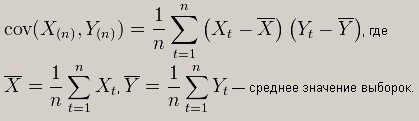Кокригинг

Кокригинг в отличие от кригинга при моделировании поверхности использует не только точки, в которых измерена моделирующая характеристика, но ещё и точки, в которых измерена другая характеристика, коррелирующая с моделируемой (изменяющаяся так же как и моделирующая). Использование кокригинга оправдано в тех случаях, когда непосредственное измерение моделируемой характеристики с необходимой плотностью является невозможным или слишком дорогостоящим при возможности дешевого измерения другой характеристики, коррелирующей с моделируемой.  

Поскольку в кокригинге используется две характеристики, то по ним строится три функции корреляции – две функции автокорреляции для каждой характеристики и одна кросс-корреляции между ними. В качестве коррелирующей функции в отличие от кригинга используется ковариация – функция от разности отклонений от среднего.

Ковариация используется вместо вариограммы потому, что позволяет оценивать корреляцию между разнородными данными за счет использования отклонения от среднего в ковариации вместо простой разности в вариограмме.

В отличие от вариограммы ковариация может иметь отрицательные значения. При ненулевом значении ковариации данные коррелируют, при нулевой нет. Для автоковариации график всегда имеет нисходящую форму, а для кросс-ковариации форма графика зависит от того, как дополнительная характеристика коррелирует относительно основной. При прямой кросс-корреляции (при увеличении основной характеристики дополнительная также увеличивается) график ниспадающий.При отрицательной кросс-корреляции (при увеличении основной характеристики дополнительная уменьшается) график возрастающий.

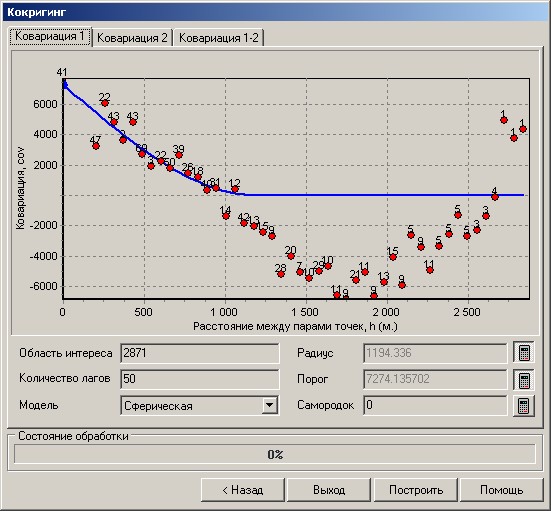
Моделирующие функции такие же, как в кригинге, только они развернуты относительно значения суммарного значения порога и самородка.

Справа теоретическая вариограмма переходит в горизонтальную нулевую прямую в точке радиуса.Поэтому радиус теоретической модели должен быть выбран в месте пересечения графика эмпирической вариограммыс горизонтальной линией нулевой ковариации.

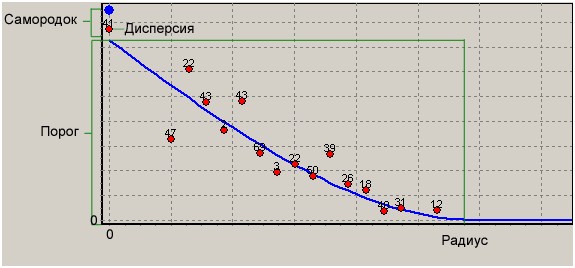
Для вариограммы в кригинге естественным ограничителем функции слева (для пар точек с нулевым взаимным расстоянием)  является ноль, так как при отсутствии ошибок расхождение значений моделирующей характеристики в одной и той же точке должно быть равно нулю. Для ковариации в общем случае это значение неизвестно, поскольку оно зависит от размера выборки. Поэтому значение самородка определить сложнее. Для этого на графике автокорелляции (внутренней корреляции) показывается значение ковариации для точек с нулевым расстоянием (на графике- точка на нулевой вертикальной оси). Для таких точек ковариация вырождается в дисперсию – среднее квадрата отклонений от среднего. Эту точку можно использовать верхним ограничителем ковариации, так же как ноль является нижним ограничителем для вариограммы (что и делается при автоматическом вычислении самородка).

Для кросс-ковариации дисперсию можно вычислить, если есть измерения обоих характеристик на одних и тех же точках. Если таких измерений нет, то нет данных для оценки взаимной ошибки разнородных измерений, поэтому значение самородка разумней установить в ноль (если нет дополнительных данных о значении взаимной ошибки).

В остальном порядок подбора теоретической ковариации такой же, как и в кригинге, только он выполняется три раза для разных графиков ковариации.

После подбора параметров модели запуск построения матрицы выполняется нажатием кнопки Построить.